27.3 Sampling distribution: Expectation

A RQ is answered using data (this is partly what is meant by evidence-based research). Fortunately, for the body-temperature study, data are available from a comprehensive American study (Shoemaker 1996).

Summarising the data is important, because the data are the means by which the RQ is answered (data below).

A graphical summary (Fig. 27.1) shows that the internal body temperature of individuals varies from person to person: this is natural variation. A numerical summary (from software) shows that:

• The sample mean is $\overline{x}={36.8051}^{\circ }$C;
• The sample standard deviation is $s={0.40732}^{\circ }$C;
• The sample size is $n=130$.

The sample mean is less than the assumed value of $\mu ={37}^{\circ }\text{C}$… The question is why: can the difference reasonably be explained by sampling variation, or not?

A 95% CI can also be computed (using software or manually): the 95% CI for $\mu$ is from ${36.73}^{\circ }$ to ${36.88}^{\circ }$C. This CI is narrow, implying that $\mu$ has been estimated with precision, so detecting even small deviations of $\mu$ from ${37}^{\circ }$ should be possible.

Show 102550100 entries

The body temperature data

	BodyTemp	Gender	HeartRate	BodyTempC
1	96.3	1	70	35.7222222222222
2	96.7	1	71	35.9444444444444
3	96.9	1	74	36.0555555555556
4	97	1	80	36.1111111111111
5	97.1	1	73	36.1666666666667
6	97.1	1	75	36.1666666666667
7	97.1	1	82	36.1666666666667
8	97.2	1	64	36.2222222222222
9	97.3	1	69	36.2777777777778
10	97.4	1	70	36.3333333333333

Showing 1 to 10 of 130 entries

Previous12345…13Next

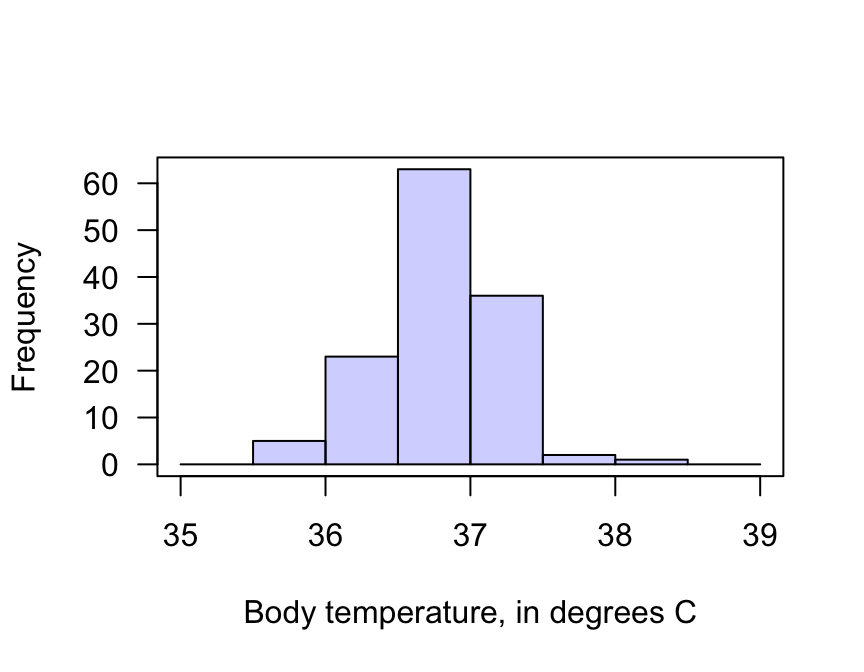
FIGURE 27.1: The histogram of the body temperature data

The decision-making process assumes that the population mean temperature is $\mu ={37.0}^{\circ }\text{C}$, as stated in the null hypothesis. Because of sampling variation, the value of $\overline{x}$ sometimes would be smaller than ${37.0}^{\circ }\text{C}$ and sometimes greater than ${37.0}^{\circ }\text{C}$.

How much variation in the value of $\overline{x}$ could be expected, simply due to sampling variation, when $\mu ={37.0}^{\circ }\text{C}$? This variation is described by the sampling distribution.

The sampling distribution of $\overline{x}$ was discussed in Sect. 22.2 (and Def. 22.1 specifically). From this, if $\mu$ really was ${37.0}^{\circ }$C and if certain conditions are true, the possible values of the sample means can be described using:

• An approximate normal distribution;
• With mean ${37.0}^{\circ }\text{C}$ (from $H_0$);
• With standard deviation of $\text{s.e.}\left(\overline{x}\right)=\frac{s}{\sqrt{n}}=\frac{0.40732}{\sqrt{130}}=0.035724$. This is the standard error of the sample means.

A picture of this sampling distribution (Fig. 27.2) shows how the sample mean varies when $n=130$, simply due to sampling variation, when $\mu ={37}^{\circ }\text{C}$. This enables questions to be asked about the likely values of $\overline{x}$ that would be found in the sample, when the population mean is $\mu ={37}^{\circ }\text{C}$.

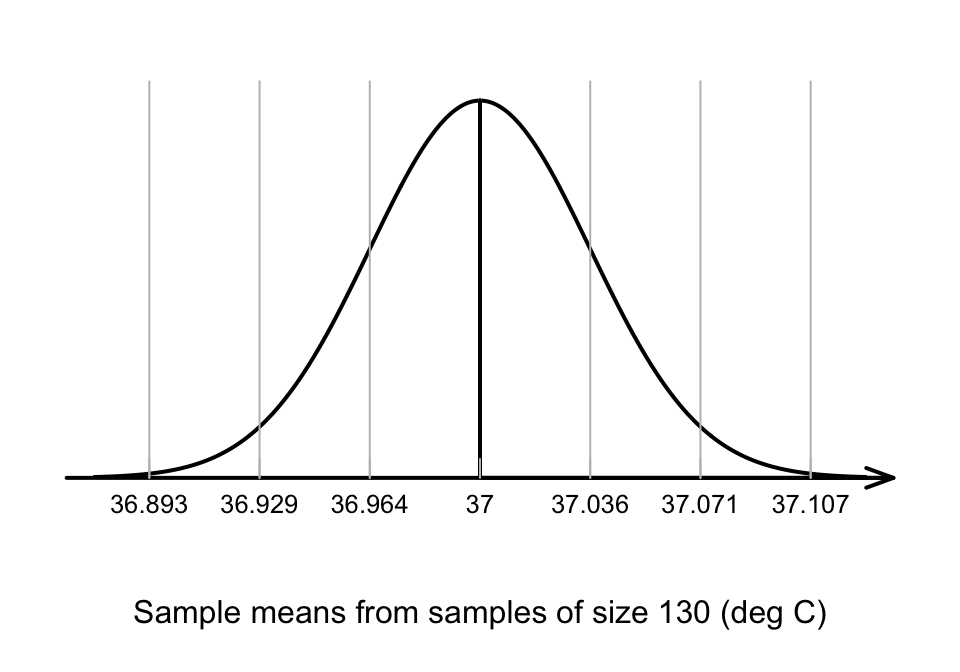
FIGURE 27.2: The distribution of sample mean body temperatures, if the population mean is ${37}^{\circ }$C and $n=130$. The grey vertical lines are 1, 2 and 3 standard deviations from the mean.

Think 27.1 (Values of $\overline{x}$) Given the sampling distribution shown in Fig. 27.2, use the 68–95–99.7 rule to determine how often will $\overline{x}$ be larger than 37.036 degrees C just because of sampling variation, if $\mu$ really is ${37}^{\circ }$C.

About 16% of the time.