27.5 $P$-values: Consistency with assumption?

This is the decision-making progress so far:

1. Assume that the population mean is ${37.0}^{\circ }\text{C}$ (this is $H_0$).
2. Based on this assumption, describe what to expect from the sample means (Fig. 27.2).
3. The observed statistic is computed, relative to what is expected using a $t$-score (Fig. 27.3): $t=-5.453$.

The value of the $t$-score shows that the value of $\overline{x}$ is highly unusual. How unusual can be assessed more precisely using a $P$-value, which is used widely in scientific research. The $P$-value is a way of measuring how unusual an observation is (if $H_0$ is true).

$P$ values can be approximated using the 68–95–99.7 rule and a diagram (Sect. 27.5.1), but more commonly by using software (Sect. 27.5.2).

27.5.1 Approximating $P$-values using the 68–95–99.7 rule

The $P$-value is the area more extreme than the calculated $t$-score. For example:

• If the calculated $t$-score was $t=-1$, the two-tailed $P$-value would be the shaded area in Fig. 27.4 (top panel): About 16%, based on the 68–95–99.7 rule. Because the alternative hypothesis is two-tailed, both sides of the mean are considered: the $P$-value would be the same if $t=+1$.

• If the calculated $t$-score was $t=-2$, the two-tailed $P$-value would be the shaded area shown in Fig. 27.4 (bottom panel): About 5%, based on the 68–95–99.7 rule. Because the alternative hypothesis is two-tailed, both sides of the mean are considered: the $P$-value would be the same if $t=+2$.

Clearly, from what the $P$-value means, a $P$-value is always between 0 and 1.

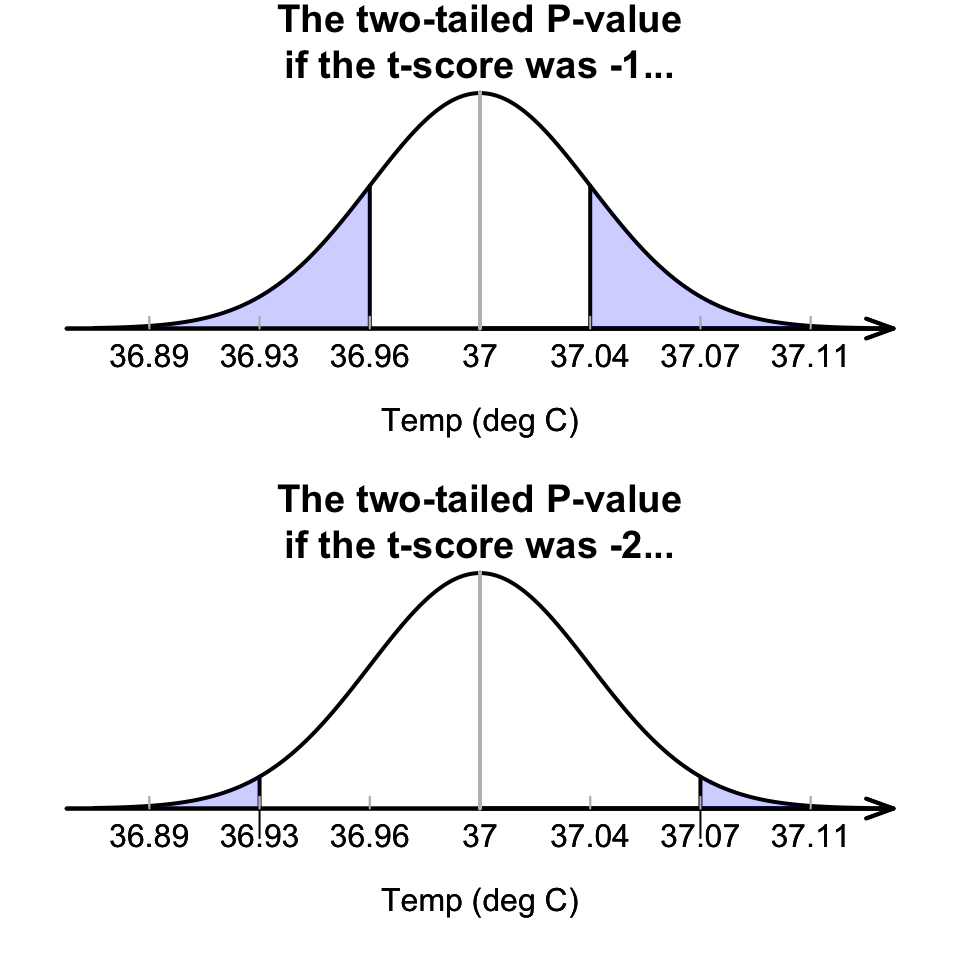
FIGURE 27.4: Computing $P$-values for the body temperature data

Think 27.2 ($P$-values) What do you think the $P$-value will be for $t=-5.45$ (using Fig. 27.3)?

Based on the 68–95–99.7 rule, the $P$-value will be extremely small.

27.5.2 Finding $P$-values using sofware

Software computes the $t$-score and a precise $P$-value (jamovi: Fig. 27.5; SPSS: Fig. 27.6). The output (in jamovi, under the heading p; in SPSS, under the heading Sig. (2-tailed)) shows that the $P$-value is indeed very small. Although SPSS reports the $P$-value as 0.000, $P$-values can never be exactly zero, so we interpret this as ‘zero to three decimal places,’ or that $P$ is less than 0.001 (written as $P<0.001$, as jamovi reports).

When software reports a $P$-value of 0.000, it really means (and we should write) $P<0.001$: That is, the $P$-value is smaller than 0.001.

This $P$-value means that, assumpting $\mu ={37.0}^{\circ }$C, observing a sample mean as low as ${36.8051}^{\circ }$C just through sampling variation (from a sample size of $n=130$) is almost impossible. And yet, we did…

Using the decision-making process, this implies that the initial assumption (the null hypothesis) is contradicted by the data: The evidence suggests that the population mean body temperature is not ${37.0}^{\circ }\text{C}$.

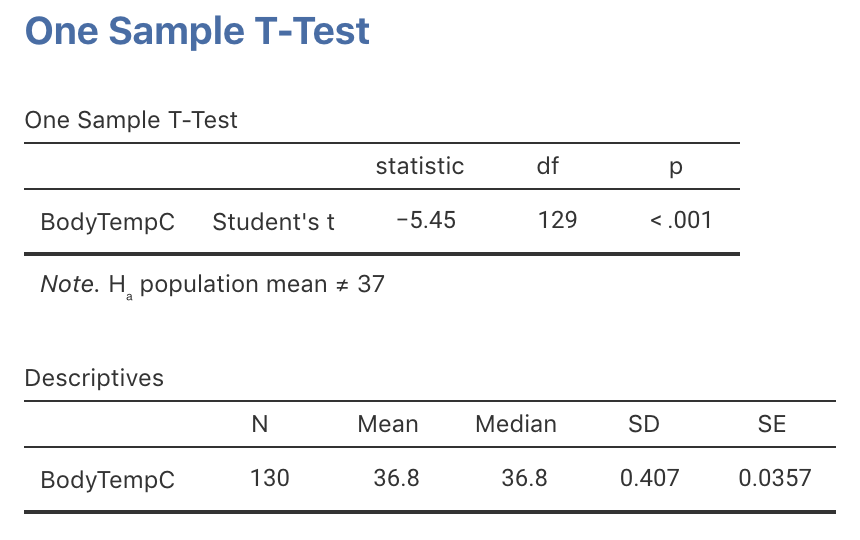
FIGURE 27.5: jamovi output for conducting the $t$-test for the body temperature data

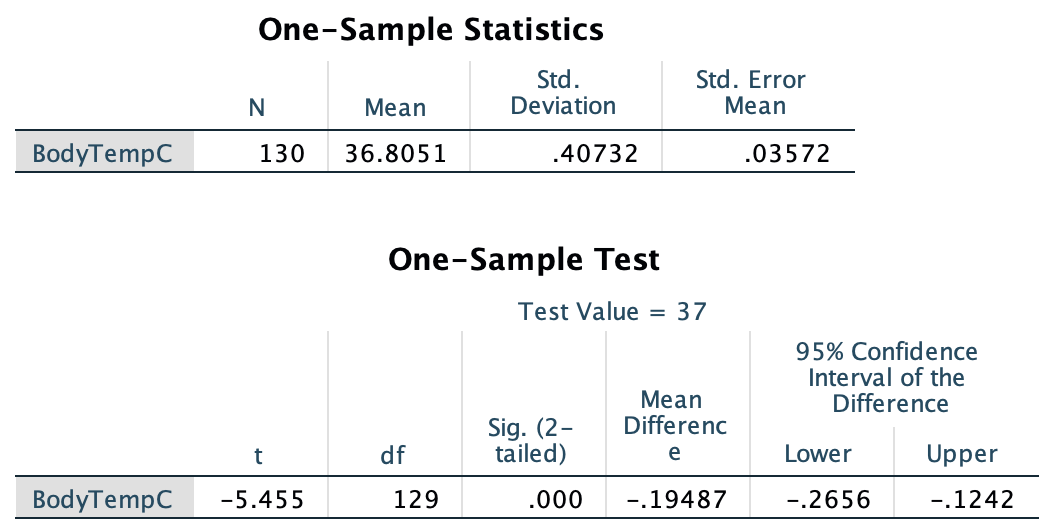
FIGURE 27.6: SPSS output for conducting the $t$-test for the body temperature data

SPSS always produces two-tailed $P$-values, calls then Significance values, and labels them as Sig.

jamovi can produce one- or two-tailed $P$-values.