D.19 Answers: CIs for one proportion

Answers to exercises in Sect. 20.11.

Answer to Exercise 20.1: \(\hat{p} = 2182/6882 = 0.317059\) and \(n=6882\). So:

\[ \text{s.e.}(\hat{p}) = \sqrt{ \frac{0.317059 \times(1 - 0.317059)}{6882} } = 0.005609244. \] The CI is \(0.317059 \pm (2\times 0.005609244)\), or \(0.317059\pm 0.01121849\).

Rounding sensibly: \(0.317\pm 0.011\) (notice we keep lots of decimal places in the working, but round the final answer).

Answer to Exercise 20.2: \(\hat{p} = 8/154 = 0.05194805\); \(\text{s.e.}(\hat{p}) = 0.0017833\); approximate 95% CI is \(0.05194 \pm (2 \times 0.0017833)\), or \(0.0519\pm 0.0358\), equivalent to 0.016 to 0.088. The CI is statistically valid.

Answer to Exercise 20.3: Use \(\hat{p} = 708/864 = 0.8194444\) and \(n=864\). Standard error: \(\text{s.e.}(\hat{p}) = 0.01308604\); approximate 95% CI is \(0.8194444 \pm (2\times 0.01308604)\). The CI is statistically valid.

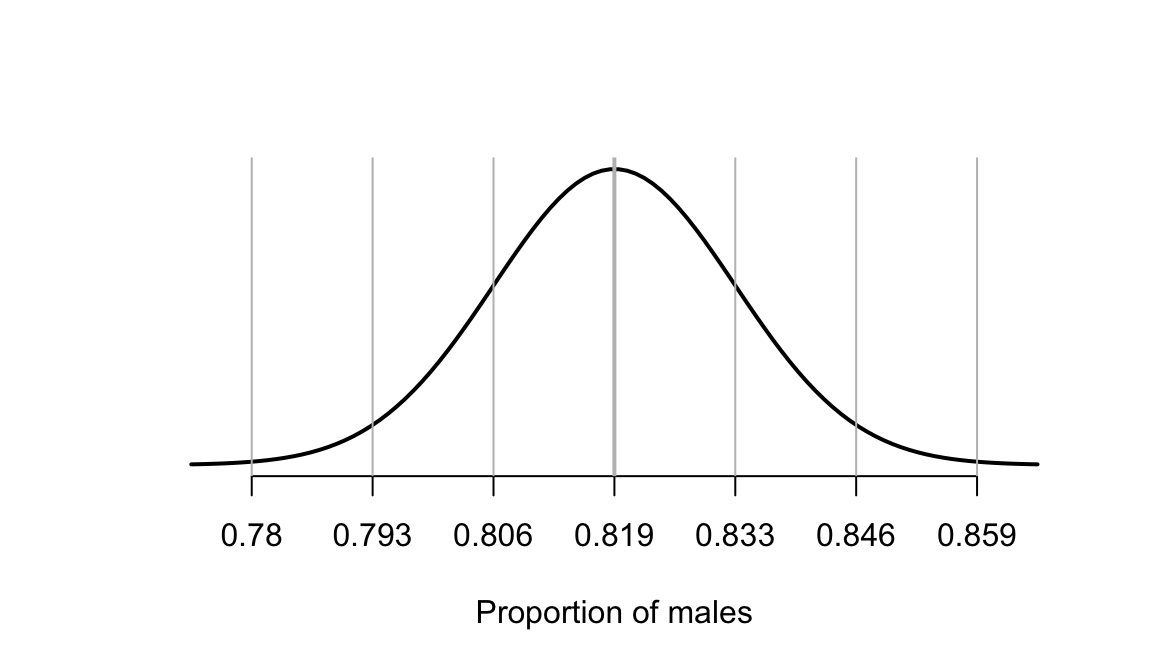
FIGURE D.6: The sampling distribution of the proportion of males in samples of 864 people with hiccups

Answer to Exercise 20.4: 1. Approximately \(n = 1/(0.05^2) = 400\). 2. Approximately \(n = 1/(0.025^2) = 1600\). 3. To halve the width of the interval, four times as many people are needed.

Answer to Exercise 20.5: After 3000 hours: \(\hat{p} = 0.2143\); \(\text{s.e.}(\hat{p}) = 0.06331\). The CI is from 0.088 to 0.341. The statistical validity conditions are satisfied.

After 400 hours: \(\hat{p} = 0\); \(\text{s.e.}(\hat{p}) = 0\). The CI is from 0 to 0: clearly silly (implies no sampling variation). This is because the statistical validity conditions are not satisfied.