17.6 Exact areas from normal distributions
Areas under normal distributions can be found using:
17.6.1 Using the hard-copy tables
To demonstration the use of the normal distribution tables, consider the percentage of observations smaller than \(z = -2\) (that is, two standard deviations below the mean) in a normal distribution.
The hard-copy tables work with \(z\)-scores to two decimal places, so consider the \(z\)-score as \(z=-2.00\). On the tables, find \(-2.0\) in the left margin of the table, and find the second decimal place (in this case, 0) in the top margin of the table (Fig. 17.6): where these intersect is the area (or probability) less than the \(z\)-score. So the probability of finding a \(z\)-score less than \(z = -2\) is 0.0228, or about 2.28%. (The online tables work differently.)
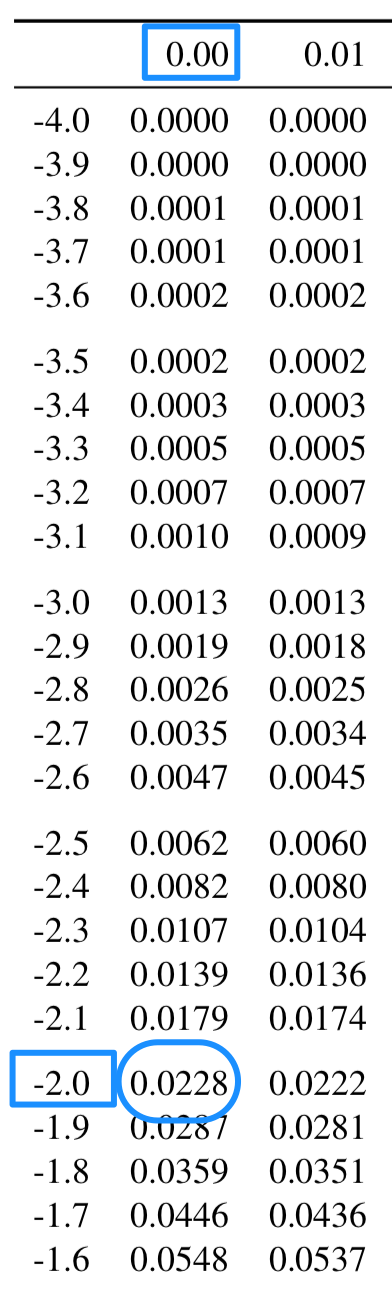
FIGURE 17.6: Using the hard-copy tables to compute the probability that \(z\) is less than \(-2\)
17.6.2 Using the online tables
The online tables work differently to the hard-copy tables. Consider the same example again: the percentage of observations smaller than \(z = -2\).
Like the hard-copy tables,
the online
tables (Appendix B.2) work
with two decimal places,
so consider the \(z\)-score as \(z=-2.00\).
In the tables,
enter the value -2 in the search region just under the column labelled z.score
(see the animation below).
After pressing Enter,
the answer is shown in the column headed Area.to.left:
the probability of finding a \(z\)-score less than \(-2\) is 0.0228, or about 2.28%.
Using either the hard-copy or online tables gives an answer of about 2.28%. Using the 68–95–99.7 rule, the answer we obtained was \(2.5\)%. Recall that the 68–95–99.7 rule is an approximation only.