34.5 Example: Removal efficiency

In wastewater treatment facilities, air from biofiltration is passed through a membrane and dissolved in water, and is transformed into harmless byproducts. The removal efficiency \(y\) (in %) may depend on the inlet temperature (in \(^\circ\)C; \(x\)).

The RQ is

In treating biofiltation wastewater, is the removal efficiency associated with the inlet temperature?

The population parameter is \(\rho\), the correlation between the removal efficiency and inlet temperature.

A scatterplot of \(n=32\) samples (Fig. 34.8) suggests an approximately linear relationship (Chitwood and Devinny 2001; Devore and Berk 2007). The output (jamovi: Fig. 34.9; SPSS: Fig. 34.10) shows that the sample correlation coefficient is \(r=0.891\), and so \(R^2 = (0.891)^2=79.4\)%. This means that about 79.4% of the variation in removal efficiency can be explained by knowing the inlet temperature.

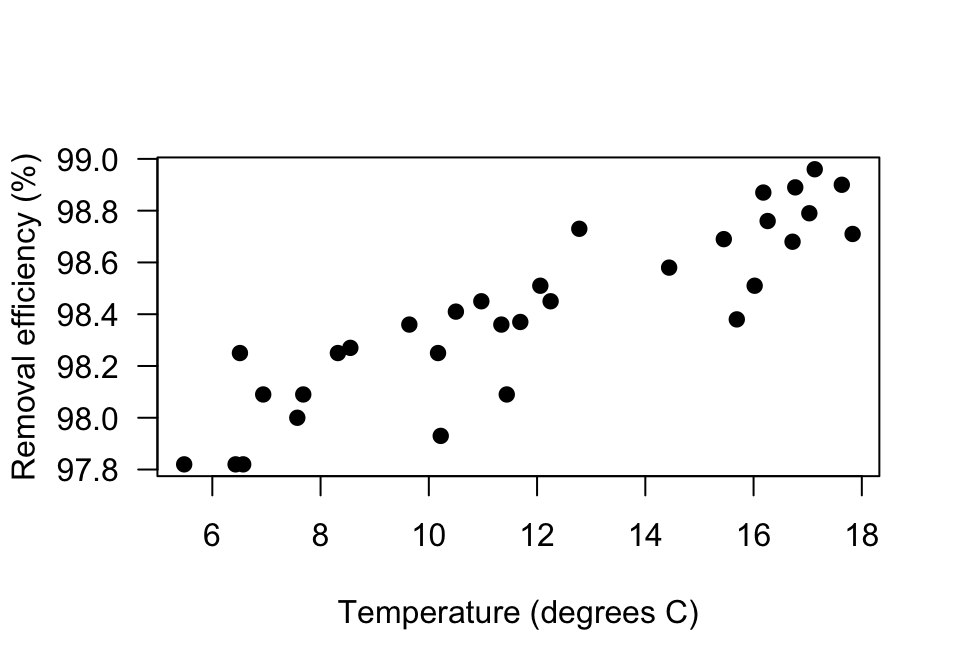
FIGURE 34.8: The relationship between removal efficiency and inlet temperature

To test if a relationship exists in the population, write:

• \(H_0\): \(\rho=0\);
• \(H_1\): \(\rho\ne0\): Two-tailed (as implied by the RQ).

The software output (jamovi: Fig. 34.9; SPSS: Fig. 34.10) shows that \(P<0.001\) (which is what \(P=0.000\) in SPSS means). We conclude:

The sample presents very strong evidence (two-tailed \(P<0.001\)) that removal efficiency depends on the inlet temperature (\(r=0.891\); \(n=32\)) in the population.

The relationship is approximately linear and there is no obvious non-constant variance, and the sample size is larger than 25, so the hypothesis test results will be statistically valid.

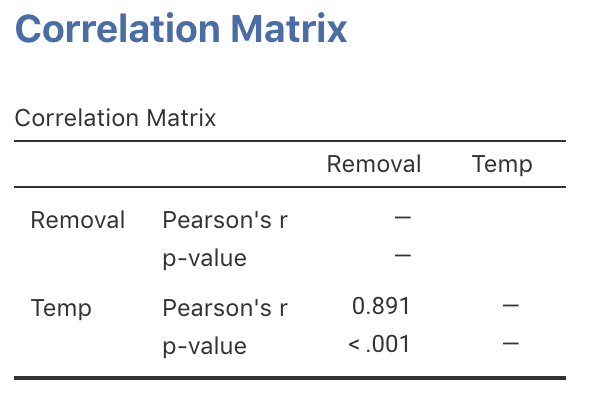
FIGURE 34.9: jamovi output for the removal-efficiency data

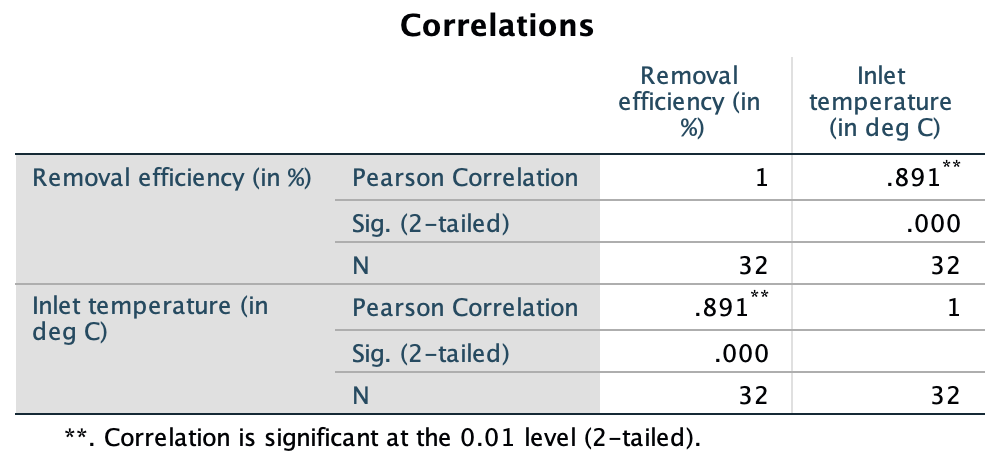
FIGURE 34.10: SPSS output for the removal-efficiency data