15.3 How decisions are made

Based on the ideas in the last section, a formal process of decision making in research can be described as follows.

TABLE 15.1: The decision-making process
Assumption Make a reasonable assumption about the value of a population parameter
Expectation Based on this assumption, describe what values of the sample statistic might reasonably be observed
Observation Observe the sample statistic. Then, if the observed sample statistic is: …unlikely to happen by chance, it contradicts the assumption.
…likely to happen by chance, it is consistent with the assumption.

To expand:

  1. Assumption: Make a reasonable assumption about the population, such as the value of a population parameter, or state a value for the population parameter to be confirmed.

  2. Expectation: Based on this assumption, describe what might be observed in the sample, such as values of the sample statistic that might reasonably be observed from all possible samples.

  3. Observation: If the observed sample statistic is:

    • unlikely to happen by chance, it contradicts the assumption about the population parameter, and the assumption is probably wrong. The evidence suggests that the assumption is wrong (but it is not certainly wrong).
    • likely to happen by chance, it is consistent with the assumption about the population parameter, and the assumption may be correct. No evidence exists to suggest the assumption is wrong (though it may be wrong).

This is one way to describe the formal process of decision making in science (Fig. 15.1).

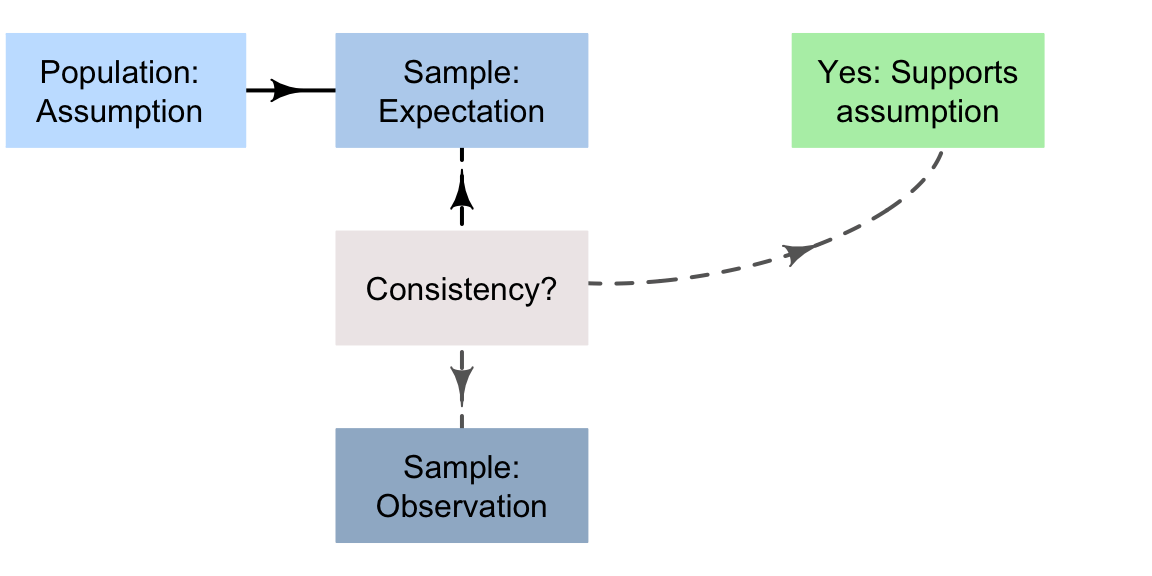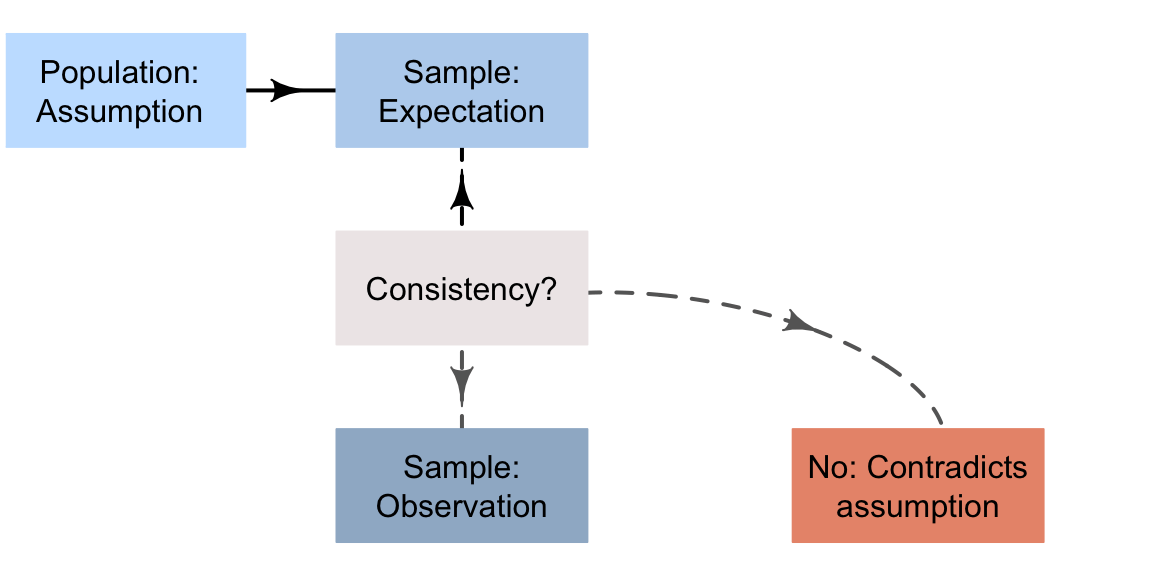
A way to make decisions

FIGURE 15.1: A way to make decisions

This approach is similar to what we use every day without really thinking about it For example, suppose I ask my son to brush his teeth (Budgett et al. 2013), and later I want to decide if he really did brush his teeth.

  1. Assumption: I assume my son brushed his teeth (because I told him to).
  2. Expectation: Based on that assumption, I expect to find a damp toothbrush when I check later.
  3. Observation: When I check later, I observe a dry toothbrush. The evidence seems to contradict my assumption, as I did not find what I expected, so my assumption is probably false: He probably didn’t brush his teeth.

Of course, I may have made the wrong decision: He may have brushed his teeth, but his brush is now dry (he may have dried his brush with a hair dryer; he’s that sort of kid). However, based on the evidence, quite probably he has not brushed his teeth.

The situation may have ended differently:

  1. Assumption: I assume my son brushed his teeth (because I told him to).
  2. Expectation: Based on that assumption, I expect to find a damp toothbrush when I check later.
  3. Observation: When I check later, I observe a damp toothbrush. The evidence seems consistent with my assumption, as I found what I expected, so my assumption is probably true: He probably did brush his teeth.

Again, I may be wrong: He may have just ran his toothbrush under a tap (again, it wouldn’t surprise me). I don’t have any evidence that he didn’t brush his teeth, though; I can hardly get him into trouble.

This logic underlies most decision making in science6.

Example 15.1 (The decision-making process) Consider the cards example from Sect. 15.2 again. The formal process might look like this:

  1. Assumption: Initially assume the pack is fair and well-shuffled pack of cards (you have no evidence to doubt this).

    In other words, the proportion of red cards is 0.5 (the value of the parameter).

  2. Expectation: Based on this assumption, roughly (but not necessarily exactly) equal numbers of red and black cards would be expected in a sample of 15 cards.

    In other words, the proportion of red cards in any sample is expected to be close to, but maybe not exactly, 0.5 (the value of the statistic).

  3. Observation: Suppose I then deal 15 cards, and all 15 are red cards.

This seems unlikely to occur if the pack is fair and well-shuffled; the data seem inconsistent with what I was expecting based on the assumption (Fig. 15.2). The evidence suggests that the assumption is probably false.

Of course, getting 15 red cards out of 15 is not impossible, so I may be wrong… but it is very unlikely. Based on the evidence, concluding that a problem exists with the pack of cards seems reasonable.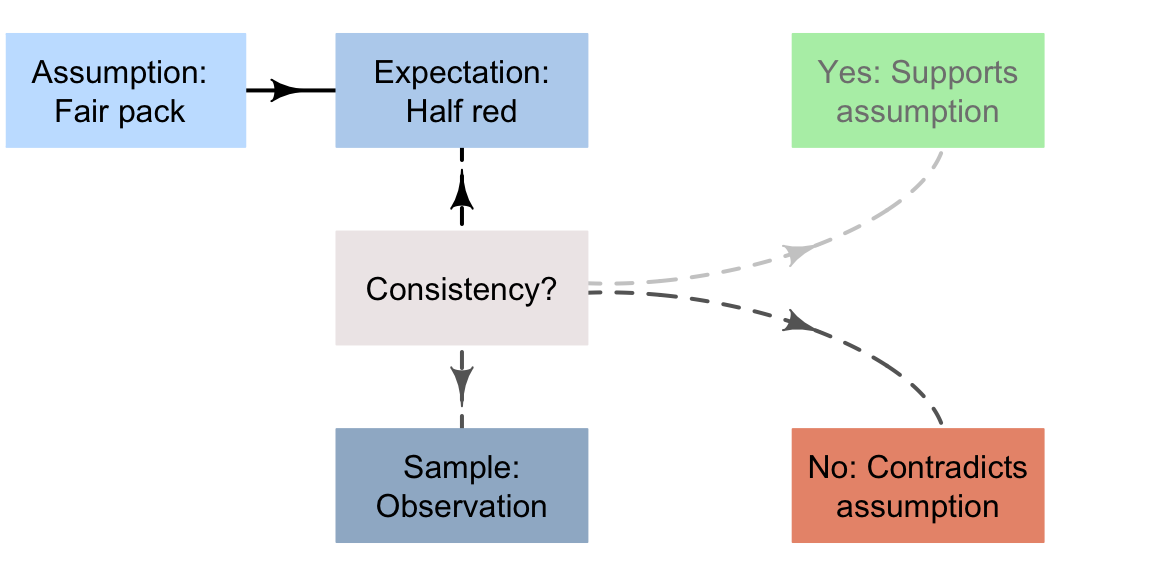
A way to make decisions for the cards example

FIGURE 15.2: A way to make decisions for the cards example

  1. Other ways exist to make decisions too, such as incorporating prior knowledge. For example, if my son had a reputation for wetting his toothbrush under the tap instead of brushing his teeth, that information can be used to help with the decision making. This approach is called Bayesian statistics, but is too advanced for this book.↩︎